NEUMANN (J. von)

NEUMANN (J. von)

L’œuvre du mathématicien John von Neumann est remarquable par la très grande variété de son champ et par l’unité conceptuelle qui s’en dégage. Héritier de Hilbert et de l’école formaliste, il sut, de ses premières recherches sur l’axiomatisation de la théorie des ensembles à la pratique des ordinateurs, justifier l’optimisme inébranlable qu’il avait placé dans le rôle privilégié des mathématiques comme niveau conceptuel. Il donna des modèles rigoureux et rationnels de théories qui semblaient informalisables dans l’optique classique de la physique en utilisant les techniques mathématiques les plus élaborées qu’il développa ou créa à cet effet.

De la mathématique à la physique nucléaire

John von Neumann naquit à Budapest d’une famille aisée. Il fit ses études supérieures à l’université de Budapest mais, pendant cette période, il séjourna fréquemment à Berlin et surtout à Zurich où il eut des contacts avec H. Weyl et G. Polya.

Ses premiers travaux mathématiques manifestent beaucoup de précocité et une grande profondeur: lorsqu’il devint privat-dozent à l’université de Berlin en 1927, il avait déjà acquis, par ses travaux sur la théorie des ensembles et les fondements de la mécanique quantique, une renommée mondiale. En 1929, il quitte Berlin pour l’université de Hambourg.

En 1931, il s’expatrie, s’établit aux États-Unis et devient professeur, à l’université de Princeton d’abord, puis, en 1933, à l’Institute for Advanced Studies de Princeton qui réunissait un grand nombre de scientifiques éminents de toutes nationalités.

Dès le commencement de la Seconde Guerre mondiale, von Neumann participe à de nombreux «projets» scientifiques militaires et paramilitaires. Il travaille sur la théorie des machines mathématiques. Comme de nombreux chercheurs américains, il a collaboré à la mise au point de la première bombe atomique, tant par ses travaux sur les calculateurs et le guidage automatique que par un travail direct avec les physiciens (étude théorique de l’implosion, contrôle des réactions thermonucléaires); en 1954, il est nommé membre de la Commission américaine de l’énergie atomique. Tombé gravement malade en 1955, von Neumann meurt à Washington à l’âge de cinquante-trois ans.

Logique mathématique

La deuxième publication de von Neumann, alors à peine âgé de vingt ans, est consacrée à un exposé, dans le système axiomatique de Zermelo, de la théorie des ordinaux. Les définitions vagues de Cantor sont remplacées par une construction précise qui évite l’introduction des types d’ordre: un nombre ordinal apparaît comme l’ensemble de tous les nombres ordinaux plus petits. Par un article de 1928 l’auteur reprendra cette étude dans un contexte axiomatique élargi.

Une série d’articles, échelonnés de 1925 à 1929, est consacrée à l’axiomatisation de la théorie des ensembles. Dans Die Axiomatisierung der Mengenlehre (1928), von Neumann propose une axiomatisation remarquablement concise et simple de la théorie naïve qui repose sur la notion d’objet de premier type (les ensembles) et de second type (les propriétés des ensembles). Il dégage clairement le rôle de l’axiome de fondation (cf. théorie axiomatique des ENSEMBLES).

La dernière publication de von Neumann sur la théorie des ensembles (1929) introduit un important axiome qui, moyennant les axiomes primitifs usuels des théories classiques, entraîne l’axiome du choix. Cet axiome de von Neumann peut s’énoncer ainsi: une propriété d’ensembles définit un ensemble d’ensembles à la seule condition qu’il n’existe pas de correspondance biunivoque entre les ensembles qui possèdent la propriété considérée et tous les ensembles.

De cette première période de l’œuvre de von Neumann, mentionnons aussi, avant d’aborder sa contribution fondamentale à l’axiomatisation de la mécanique quantique, un important article de 1927 consacré à la non-contradiction des mathématiques (dans le cadre des méthodes finitistes de Hilbert) et des travaux sur la «pathologie» de la théorie de la mesure: extension à des groupes assez généraux des résultats de F. Hausdorff, S. Banach et A. Tarski sur la mesure universelle et les décompositions paradoxales de la sphère ^{[cf. BANACH (S.)]}. Von Neumann s’est d’ailleurs intéressé toute sa vie à la théorie de la mesure et on lui doit des démonstrations de l’existence de la mesure de Haar sur un groupe localement compact et du théorème de Radon-Nykodym sur la «dérivation» d’une mesure par rapport à une autre.

Mathématiques et physique théorique

Le programme formaliste de Hilbert allait être illustré avec un succès éclatant dans l’axiomatisation de la mécanique quantique réalisée par von Neumann de 1927 à 1929. Les résultats de ces travaux sont rassemblés dans Mathematische Grundlagen der Quantenmechanik , publié en 1932, ouvrage qui est devenu un grand traité classique.

Von Neumann prend l’espace de Hilbert comme cadre mathématique pour exprimer les concepts quantiques sur la nature des mesures en physique, les opérateurs de l’espace de Hilbert correspondant aux «observables» de la physique relativiste (cf. mécanique QUANTIQUE). Les opérateurs qui s’introduisent ainsi sont hermitiens mais non bornés , donc ne sont pas redevables de la théorie classique de Hilbert (cf. théorie SPECTRALE). Von Neumann étendit la théorie spectrale aux opérateurs non bornés auto-adjoints , tandis que le cas général le conduisait à une étude mathématique détaillée des transformations symétriques non auto-adjointes. Dans un article de 1929, il introduit et décrit en détail les algèbres d’opérateurs appelées de nos jours W-algèbres ou aussi «algèbres de von Neumann». Les tentatives d’utilisation des treillis dans la classification des facteurs des algèbres d’opérateurs le conduisirent à des recherches sur la théorie des treillis; on lui doit dans ce domaine les deux notions importantes de géométries continues et d’anneaux réguliers .

Dès 1927, von Neumann donne une analyse mathématique de la mécanique quantique en des termes entièrement probabilistes: le concept de matrice statistique de von Neumann, pour décrire simultanément plusieurs systèmes qui ne sont pas au même niveau quantique, est devenu un outil essentiel ^{[cf. STATISTIQUE]}. Il utilise ces toutes nouvelles notions pour fonder mathématiquement la thermodynamique quantique. Ce sont des problèmes issus de la thermodynamique qui le conduisirent, en 1931, presque simultanément avec G. Birkhoff, à élaborer la théorie ergodique sous sa forme moderne (cf. théorie ERGODIQUE).

Pour replacer l’œuvre de von Neumann dans son contexte novateur, citons S. Ulam: «Les idées de la physique du XIX^e siècle, dominées mathématiquement par les équations différentielles et intégrales et la théorie des fonctions analytiques, étaient devenues insuffisantes. La nouvelle théorie quantique avait besoin d’un point de vue théorique plus général, les notions primitives elles-mêmes incluant déjà des distributions probabilistes et des espaces fonctionnels de dimension infinie [...]. L’œuvre de von Neumann vint à un moment où tout le complexe d’idées issu de la théorie des ensembles de Cantor et des travaux algébriques des plus grands mathématiciens du début du siècle pouvait être exploité dans ce but.»

Théorie des jeux et mathématiques économiques

Bien que certains jeux stratégiques aient été abordés par E. Borel, c’est von Neumann et son collègue de Princeton, l’économiste autrichien O. Morgenstern, qui sont les véritables créateurs de la théorie mathématique des jeux avec leur célèbre Theory of Games and Economic Behavior (1944): cet ouvrage contient le résultat central de la théorie, le théorème du minimax. Ce volumineux traité avait été préparé par un article de von Neumann où, dès 1928, il posait les fondements conceptuels de son approche (cf. théorie des JEUX, HASARD).

Le problème du choix d’une stratégie est lié à la notion de «résultat le plus favorable» qui est une notion délicate (cf. théorie des JEUX, chap. 1), et von Neumann fut amené à se pencher en mathématicien sur la notion d’«utilité». On lui doit le théorème suivant, qu’on énoncera explicitement car il joue un rôle important dans les sciences humaines.

Existence d’une fonction d’utilité

Soit X un ensemble sur lequel on a défini une «relation de préférence» 僚 telle que:

(1) Quels que soient x , y 捻 X, on a une, et une seule, des trois situations x = y , x 僚 y ou y 僚 x ;

(2) Si x 僚 y et y 僚 z , alors x 僚 z . On suppose qu’il existe une opération qui, à tous x , y 捻 X et à tout nombre réel 見, 0 麗 見 麗 1, fait correspondre un élément de X noté (formellement) 見x + (1 漣 見)y , avec les propriétés:

(5) Si x 僚 y , alors x 僚 見x + (1 漣 見)y 僚 y pour tout 見;

(6) Si x 僚 y 僚 z , alors il existe 見 et 廓 tels que:

Alors, il existe une fonction u : XR (unique à un facteur près) telle que:

(7) Si x 僚 y , alors u (x ) 礪 u (y );

(8) Pour tous x , y 捻 X et 見, on a:

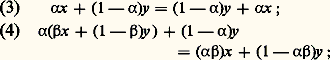
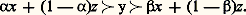
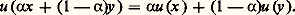La théorie des jeux s’applique de manière naturelle aux situations économiques qui sont compétitives. On doit à von Neumann un modèle mathématique de l’équilibre économique et des conditions d’existence d’une telle situation.

Machines mathématiques

Von Neumann consacra la dernière partie de sa vie aux problèmes de logique et d’analyse numérique posés par les calculateurs. Il réalisa une étude théorique du problème de la programmation , c’est-à-dire de la transformation d’un problème mathématique en un système codé d’instructions, et de très nombreuses méthodes particulières, pour la résolution de problèmes d’analyse numérique comme l’inversion des matrices d’ordre élevé par exemple.

Ses premiers travaux de logique mathématique prédisposaient von Neumann à une analyse théorique de la notion de machine. On peut citer des articles consacrés à la structure formelle des automates, aux machines reproductrices, c’est-à-dire capables de construire des machines identiques ou mieux des machines dont la complexité croîtrait de «génération en génération» (par adaptation à l’environnement par exemple), aux relations structurelles entre le système nerveux central de l’homme et les machines.

Encyclopédie Universelle. 2012.